یادگیری عمیق
دانشگاه فردوسی مشهد
محمود امینطوسی
Deep Learning
Mahmood Amintoosi
پاییز ۱۴۰۲
Source book
Deep Learning with Python,by: FRANÇOIS CHOLLET

https://www.manning.com/books/deep-learning-with-python-second-edition
LiveBook
Github: Jupyter Notebooks
Chapter 2
Before we begin: the mathematical building blocks of neural networks
This chapter covers:
- A first example of a neural network
- Tensors and tensor operations
- How neural networks learn via backpropagation and gradient descent
We will use Python in examples
| Python Data Science Handbook. Essential Tools for Working with Data by: Jake VanderPlas |

|
- Read the book in its entirety online at https://jakevdp.github.io/PythonDataScienceHandbook/
- The book's Jupyter notebooks: https://github.com/jakevdp/PythonDataScienceHandbook
A first look at a neural network
IRIS Classification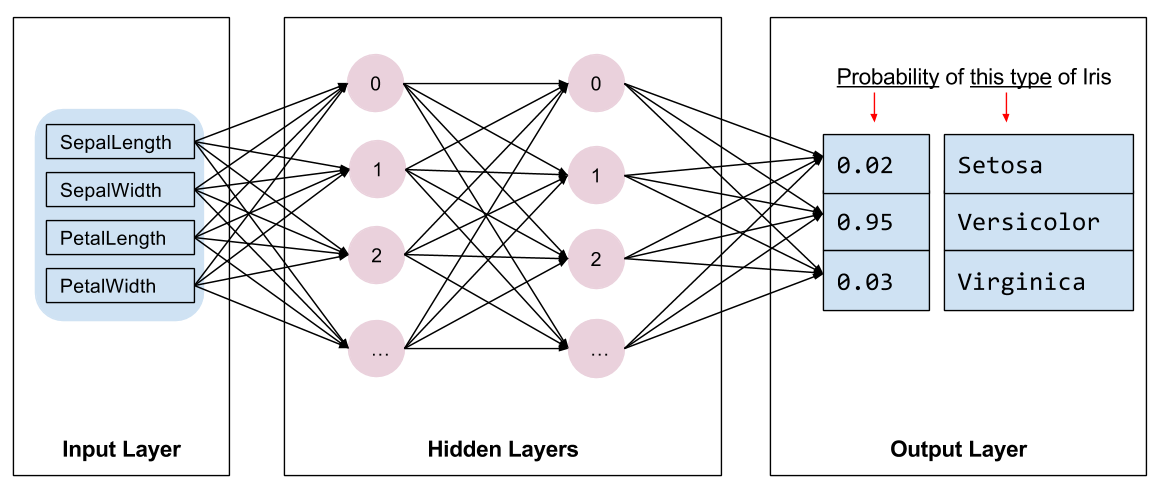
Source: Tensorflow.org
2.1-a-first-look-at-a-neural-network
Digits Classification
from tensorflow.keras.datasets import mnist
(train_images, train_labels), (test_images, test_labels) = mnist.load_data()
from tensorflow import keras
from tensorflow.keras import layers
model = keras.Sequential([
layers.Dense(512, activation="relu"),
layers.Dense(10, activation="softmax")
])
model.compile(optimizer="rmsprop",
loss="sparse_categorical_crossentropy",
metrics=["accuracy"])
train_images = train_images.reshape((60000, 28 * 28))
train_images = train_images.astype("float32") / 255
test_images = test_images.reshape((10000, 28 * 28))
test_images = test_images.astype("float32") / 255
model.fit(train_images, train_labels, epochs=5, batch_size=128)
test_digits = test_images[0:10]
predictions = model.predict(test_digits)
predictions[0]
predictions[0].argmax()
Compilation step
- An optimizer—The mechanism through which the network will update itself based on the data it sees and its loss function.
- A loss function—How the network will be able to measure its performance on the training data, and thus how it will be able to steer itself in the right direction.
- Metrics to monitor during training and testing—Here, we’ll only care about accuracy (the fraction of the images that were correctly classified)
Data representations for neural networks
Tensors
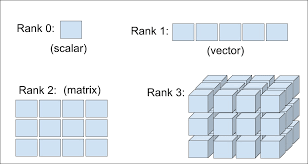
Don’t confuse a 5D vector with a 5D tensor! A 5D vector has only one axis and has five dimensions along its axis, whereas a 5D tensor has five axes (and may have any number of dimensions along each axis).
Dimensionality can denote either the number of entries along a specific axis (as in the case of our 5D vector) or the number of axes in a tensor (such as a 5D tensor), which can be confusing at times. In the latter case, it’s technically more correct to talk about a tensor of rank 5 (the rank of a tensor being the number of axes), but the ambiguous notation 5D tensor is common regardless.
2.2.6 Manipulating tensors in Numpy
my_slice = train_images[:, 14:, 14:]
2.2.7 The notion of data batches
batch = train_images[128 * n:128 * (n + 1)]
2.2.8 Real-world examples of data tensors
- Vector data—2D tensors of shape
- Timeseries data or sequence data—3D tensors of shape
- Images—4D tensors of shape
- Video—5D tensors of shape
(samples, features)
(samples, timesteps, features)
(samples, height, width, channels) or
(samples, channels, height, width)
(samples, frames, height, width, channels) or
(samples, frames, channels, height, width)
The gears of neural networks: tensor operations
- Element-wise operations
- Broadcasting
- Tensor dot
- Tensor reshaping
Tensor Operations
2.3-Tensor-Operations
import numpy as np
x = np.random.random((3, 2))
print(x)
y = np.ones((2,))/2
print(y)
z = np.maximum(x, y)
print(z.shape)
print(z)
z = x+y
print(z)
z = x*y
print(z)
A geometric interpretation of deep learning

The engine of neural networks: gradient-based optimization
- What’s a derivative?
- Derivative of a tensor operation: the gradient
- Stochastic gradient descent
- Chaining derivatives: the Backpropagation algorithm
Intro to optimization in deep learning
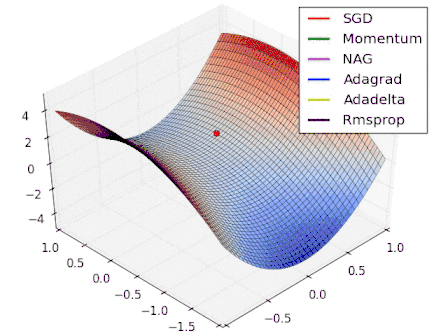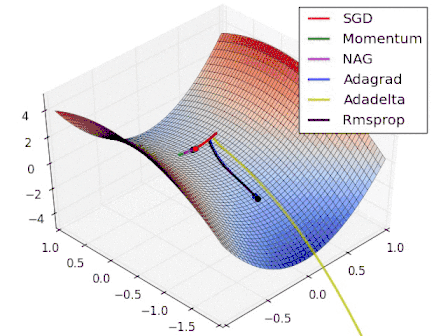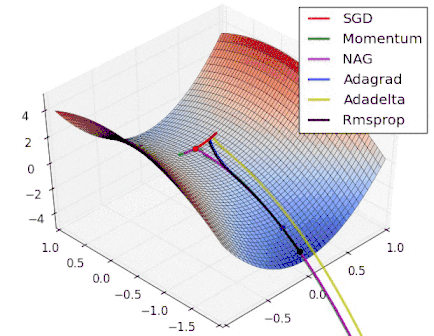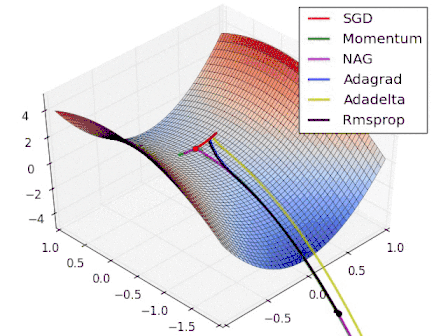
Various Gradient Descent Algorithms
Stochastic Gradient Descent
|

|
TensorFlow Operations
Auto Gradient in TF2
import tensorflow as tf
x = tf.constant(3.0)
with tf.GradientTape(persistent=True) as g:
g.watch(x)
y = x * x
z = y * y
dy_dx = g.gradient(y, x) # 6.0
dz_dx = g.gradient(z, x) # 108.0 (4*x^3 at x = 3)
dz_dy = g.gradient(z, y) # 18.0 (2*y at y = 9)
del g # Drop the reference to the tape
print(dy_dx)
print(dz_dx)
print(dz_dy)
tf.Tensor(6.0, shape=(), dtype=float32)
tf.Tensor(108.0, shape=(), dtype=float32)
tf.Tensor(18.0, shape=(), dtype=float32)
- Questions? -
m.amintoosi @ gmail.com
webpage : http://mamintoosi.ir
webpage in github : http://mamintoosi-cs.github.io
github : mamintoosi